43-剪裁算法—前置几何知识
Created|Updated|图形学工程&工业仿真1-图形学，从0构建一个opengl软光栅
|Post Views:
直线方程理解
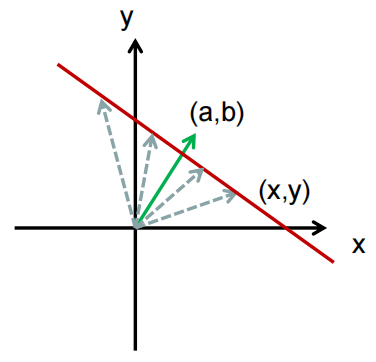
一般直线方程写作:
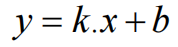
由此也存在直线方程写作:
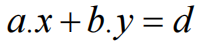
上式可分解为向量点乘，向量(a,b)必须为归一化后的向量
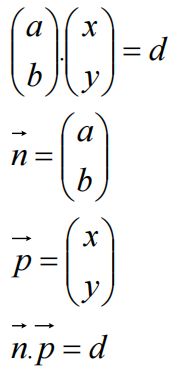
当向量n为单位向量，n向量乘以p向量得到的p向量是n向量方向的投影长度
该表达式可理解为，p点是所有满足向量n投影长度为d的点集合
直线方程距离理解
直线表达式中的d发生变化的时候，意味着直线沿着法线n滑动
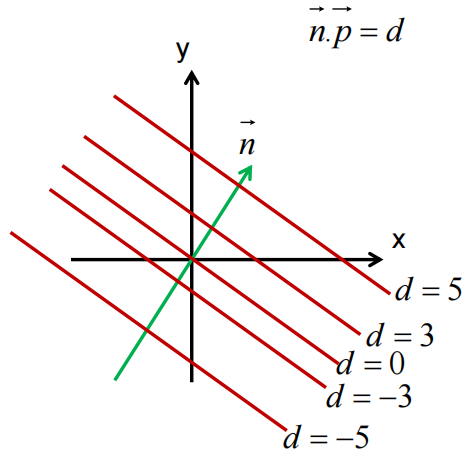
点与直线的距离关系
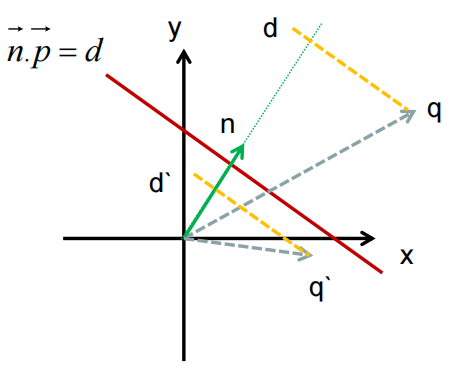
空间中任一点q，带入到直线方程，得到的结果都是q在n上的投影
表示q在直线法线的一侧，即正面
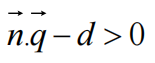
表示q在直线法线对侧，即背面
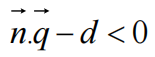
平面方程
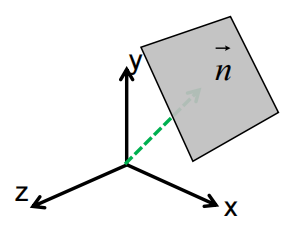
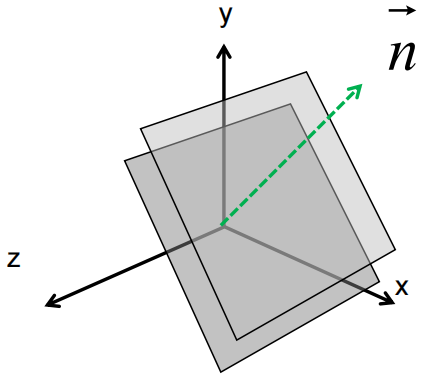
空间中一平面，使用法线方式进行表示如下:
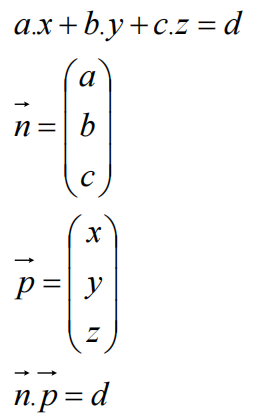
平面方程理解
平面方程的d发生变化时，意味着平面沿着法线n方向滑动
点与平面的距离关系
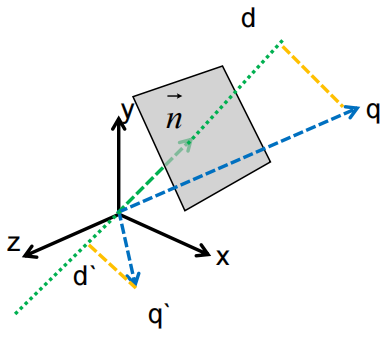
表示q在平面法线的一侧，即正面
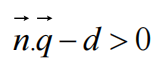
表示q在平面法线的对侧，即背面
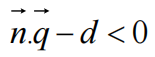
Author: LYJ
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
Related Articles
2025-09-21
44-剪裁算法
目标分析分析对于一个Mesh的一次Draw调用，其中的三角形会产生以下三种情况 1.三角形在可视范围内，顶点都保留2.三角形在与视范围相交，去掉外围点，产生新点3.三角形不在可视范围内，丢弃所有顶点 Sutherland-Hodgman算法也叫逐边剪裁法，该算法采用了分割处理、逐边剪裁的方法 算法思想（二维） 一次用窗口的一条边所在直线裁剪多边形，循环多次； 每次，构造一个空的点数组DST；原数组为SRC 每次，所有顶点从0号开始，作为S点，S后面的点为P点，依次进行测试，结果输出点到DST，剪裁原则如下： Sutherland-Hodgman算法举例演示（1） 输入0-1-2考察右侧边 如法炮制考察剩余三边后，输出三角形0`-1-1`的点 Sutherland-Hodgman算法举例演示（2） 输入0-1-2考察上侧边 如法炮制考察剩余三边后，输出0`-1-2-2` 输入0`-1-2-2`考察右侧边 如法炮制考察剩余三边后，输出1-1`-2``-0` 对其他两条边如法炮制，最终可以获得下方所示数组： 接下来进行三角形重建：永远以数组第一个顶...
2025-09-22
45-剪裁算法代码实现
内容1.Clipper类以及sutherlandHodgman算法2.GPU绘制流程加入剪裁3.绘制示例 dataStructures.h#pragma once#include "../global/base.h"#include "../math/math.h"//VAO之中，用于描述属性读取方式的Descriptionstruct BindingDescription { uint32_t mVboId{ 0 }; size_t mItemSize{ 0 }; size_t mStride{ 0 }; size_t mOffset{ 0 };};struct VsOutput { math::vec4f mPosition{ 0.0f, 0.0f, 0.0f, 1.0f }; math::vec4f mColor;//此处颜色改为0.0...
2025-09-23
46-透视修正算法
插值算法回顾透视投影下，目前代码中，都是变化到屏幕空间坐标系后，按照屏幕空间形成的三角形对某点进行重心坐标插值： 但是在三维空间中，三角形是立体有深度(前后)的图形，需要使用空间中的三角形重心坐标，使用屏幕上二维的重心坐标是不准确的 问题分析（1）逆着y轴看下去，可以得到如下平面视图： 由上图可知，在屏幕空间中，A`O`:B`O`=7:3在三维空间中，AO:BO=5:5可见两者的重心坐标并不相等，因此需要透视修正：为了能方便计算屏幕空间三角形像素的重心坐标，需要找到一种方法计算三维空间对应点的重心坐标 问题分析（2）顶点到屏幕，会经历如下空间变换： 我们已经知道三维空间投影到二维重心坐标会变换，那么N空间到S空间，对应点的重心坐标会发生变换吗？ 如上图分析，N空间到S空间，会发生两个变换：（1）顶点坐标从-1到1，变换为0-1，这个过程NDC内对应顶点重心坐标不会发生改变（2）顶点坐标从为0-1变化为屏幕上具体的像素点，并且由于width与height不同，产生了横向与纵向的拉伸，可以理解为，先投影到1*1的幕布上，然后横向统一缩放width倍...
2025-09-24
47-透视修正代码实现
内容1、修改了GPU中的透视除法函数2、加入剪裁函数trim3、加入透视恢复函数4、Raster插值，加入1/w以及depth5、主流程更改6、示例 修改GPU中的透视除法函数dataStructures.h修改了GPU中的透视除法函数，添加了mOneOverW代表当前点的1/w #pragma once#include "../global/base.h"#include "../math/math.h"//VAO之中，用于描述属性读取方式的Descriptionstruct BindingDescription { uint32_t mVboId{ 0 }; size_t mItemSize{ 0 }; size_t mStride{ 0 }; size_t mOffset{ 0 };};struct VsOutput { float mOneOverW{ 0.0f }; math:...
2025-09-26
49-深度测试算法与代码实现
问题分析：在绘制两个三角形的过程中，系统如何决定谁遮挡谁？ 之前我们的设计是画家算法，即最早渲染的被最新渲染的遮挡，但不按照由远到近的顺序绘制时，就得不到我们像要的效果，如何直接根据图形的远近设置他们是否被遮挡，我们需要深度测试算法 深度在屏幕空间变换后，我们得到的每个顶点的z坐标即顶点深度；在经过光栅化后得到的每个像素中都记录则经过插值的搭配的z值，即像素的深度值，用于描述当前像素距观察点有多远深度取值范围是0-1 深度检测： 对于当前像素，都需要跟画布已有的像素深度值进行对比，如果被挡住则丢弃；如果靠前则保留 深度缓存：跟画布一样分辨率大小的内存空间，用于记录画布上已经绘制的每个像素的深度值 深度测试算法解析 深度缓存与颜色缓存分辨率一致，初始化为1.0f 三角形每个像素深度值与深度缓存中对应深度值对比；如果三角形像素深度值较小（接近观测点）则通过测试；通过测试的像素，使用新的像素深度值覆盖对应的深度值；通过测试的像素，可以绘制到颜色缓存 API设计深度检测可配置参数较多，我们只选取深度对比函数进行编写：DEPTH_LESS: 代表比现存深度小才能通过检测DEPTH_GR...
2025-09-25
48-背面剔除算法与代码实现
剔除算法目的：提前丢弃对最终画面无贡献的三角形，减少不必要的渲染计算 OpenGL中，系统API允许设置三角形剔除：1、设置“正面”三角形的顶点连接方式（顺时针/逆时针）2、设置剔除“正面”还是剔除“背面” 举例： 顶点逆时针连接维正面/剔除背面 左手坐标系问题在NDC坐标中，已经变成了采用左手坐标系表示在左手坐标系中，向量叉乘必须采用左手来判定叉乘结果向量方向，例如：x与y叉乘，得到z 判定算法举例：逆时针为正面，剔除背面以0点为起点，与1点/2点构成两条边e1/e2求两向量叉乘，e1叉乘e2（左手坐标系）叉乘结果冲向屏幕内部，左手坐标系下，为z正方向，即z>0则使用z>0可判定该三角形可保留 若如下图，顺时针排列顶点，e1与e2叉乘得到z<0，则可判定剔除该三角形 总结以0点为起点，与1点/2点构成两条边e1/e2；计算e1与e2叉乘，得到其结果z值分条件判定：1、剪裁背面/逆时针为正面: z>0 保留2、剪裁正面/逆时针为正面: z<0 保留3、剪裁背面&#...
Announcement
This is Seagull Blog
Post Series