27-空间变换—变换矩阵的本质

详解基向量

空间中的一组线性无关向量，即可构成一组基向量
点P的坐标只有放在某一个基向量构成的坐标系中才会有意义

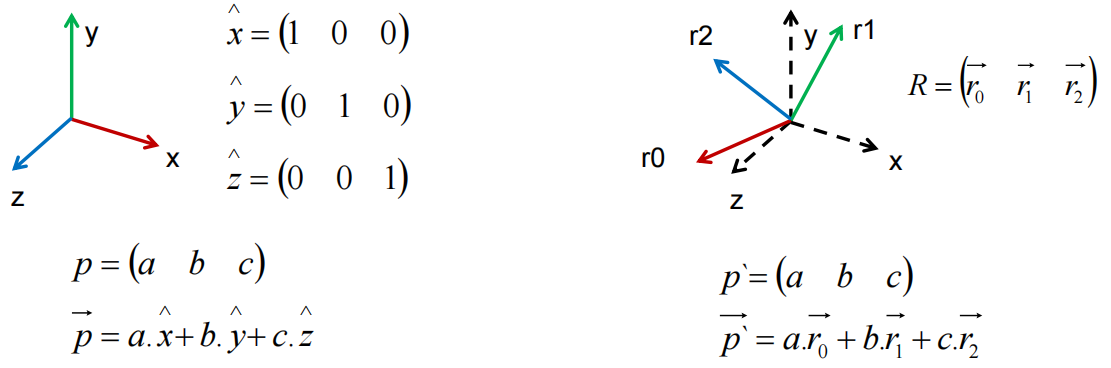
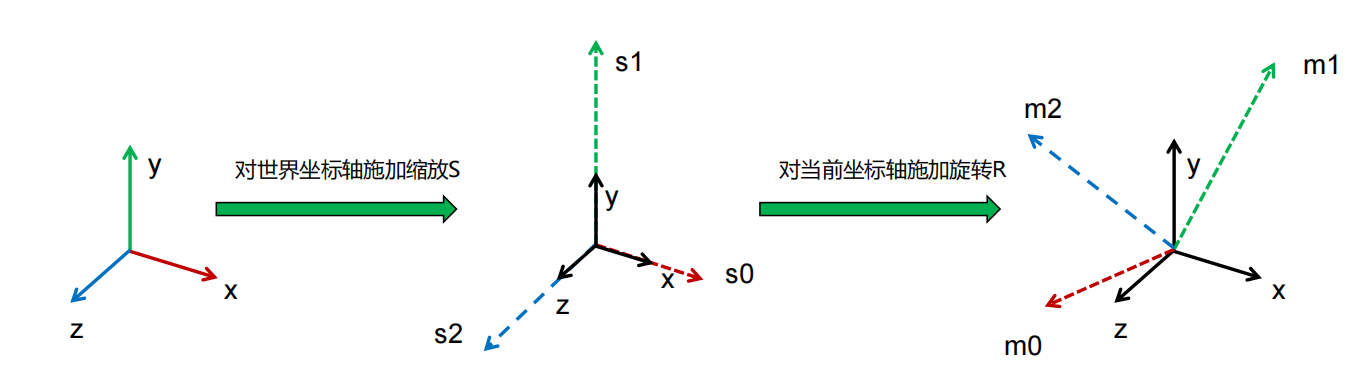
局部坐标系与世界坐标系

世界坐标系: 定义一组线性无关/模为1/互相垂直的向量，作为整个世界的中心坐标系（笛卡尔坐标系）

局部（模型）坐标系： 对世界坐标系的三个基向量进行变换后，得到的坐标系（一开始与世界坐标系重合）

点P局部坐标与世界坐标

世界坐标: 点P在世界坐标系中的坐标
局部（模型）坐标: 在转换后新形成的一组基向量构建的坐标系中点P的坐标

P初始状态下，其局部坐标系与世界坐标系重合； P当前在世界/局部坐标系中的坐标为（a,b,c）； 经过旋转变换后， P的局部坐标系跟随旋转，变成了旋转矩阵的三个列向量， P在局部（模型）坐标系中的坐标仍是（a,b,c）， P在世界坐标系中的坐标为：

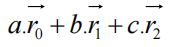
变换矩阵的相互作用

举例： 先使用S矩阵对坐标进行缩放，再使用R对其进行旋转

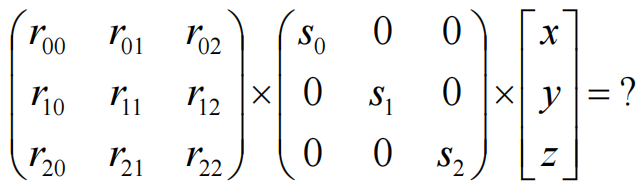
根据矩阵运算结合律，可以先把S与R相乘，再集体作用到目标点；二者相乘得到如下的矩阵M

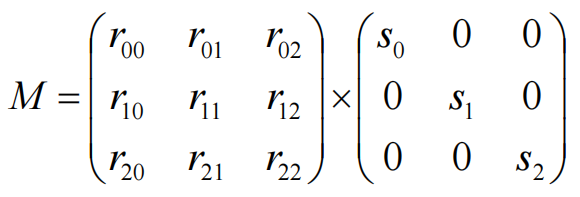
根据列视图可知S矩阵的每一列，都会作为一组调配因子对R中的列向量进行组合，坐标即调配因子:

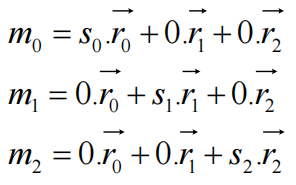
S的三个基向量构成一个局部坐标系，把S的三个基向量按照R进行旋转得到的就是M

S的三个基向量在R张成的坐标系中，坐标不变，但是在世界坐标系中发生了改变

P`在局部坐标系的坐标仍然是（a,b,c）

P`在世界坐标系的坐标就是（a,b,c）对R张成的局部坐标系的三个基向量的调配

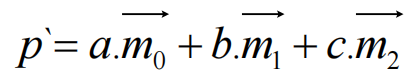
延申理解

对于如下连续矩阵变换:

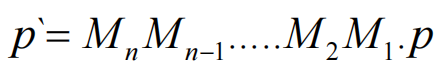
抽出所有变换矩阵，如下表达:

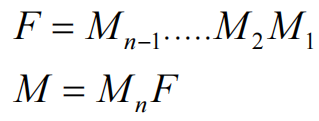
相当于前方n-1个矩阵相乘，组成了一组基向量

最后Mn对F的每个基向量进行变换，形成最终M矩阵每个列向量，从而形成新的局部坐标系

结论

对一个矩阵A做变换B（矩阵相当于坐标系，作用于变换矩阵就是更改这个坐标系，坐标系上的某个点就一组列向量），相当于把A矩阵的每一个列向量做了B变换，形成一组新的基向量，按列排列形成M矩阵，最终用M的列向量为基，计算P点的世界坐标就是通过原世界坐标（因为点P相对于局部坐标不变，所以使用原世界坐标）来调配这个基向量得到P在世界坐标系中的新坐标；多变换相乘，即从右往左，逐步变更基向量的过程