19-矩阵行列式的几何意义

基向量

描述一个三维空间中所有的点，就需要一个基础的坐标系，比如xyz三个轴，由(1,0,0)/(0,1,0)/(0,0,1)三个向量代表，构成了三维空间的一组基

空间中所有的点坐标都可以表示为这一组基向量的线性组合，比如(3,1,2)这个点可以表示为:

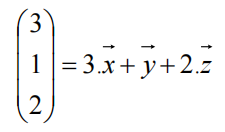
三维空间也可以存在其他的基向量组的选择，比如(1,1,0)/(0,1,1)/(1,0,1)

一个三维矩阵的列向量，也按序构成了一组基向量

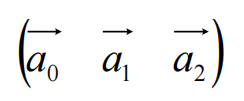
行列式几何意义

一个矩阵可以看作多个列(行)向量的组合
只考虑二维和三维行列式：
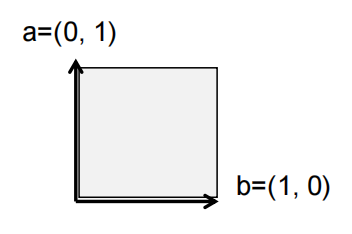
（1）二维矩阵行列式是列(行)向量张成的平行四边形的有符号面积
（2）三维矩阵行列式是列(行)向量张成的平行六面体的有符号体积

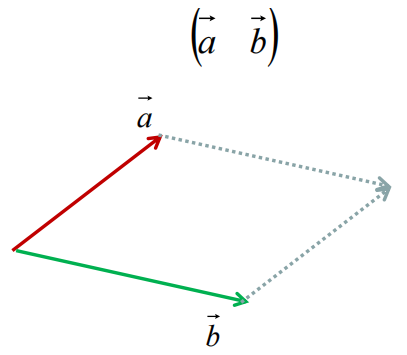
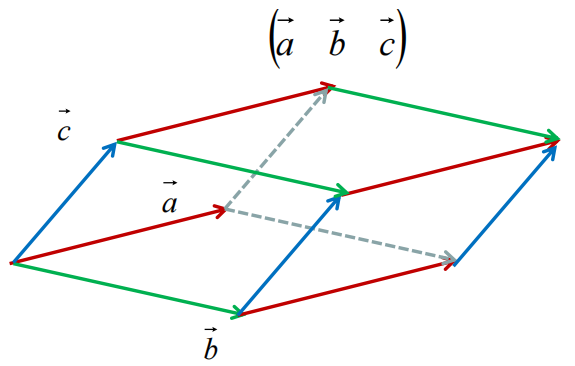
有向面积

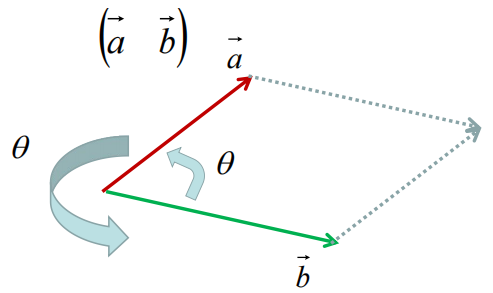
当我们的矩阵列是a与b两个向量构成时，需要计算其面积，就可以使用向量的叉乘(二维情况下与叉乘算法一致)，即如下公式

（1）如果是b与a顺序的叉乘(逆时针)，则角度在180以内，sin值为正 （2）如果是a与b顺序的叉乘(顺时针)，则角度在180度以外，sin值为负

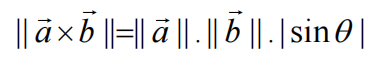
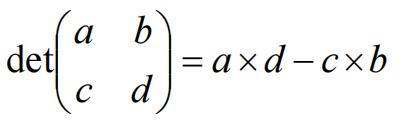
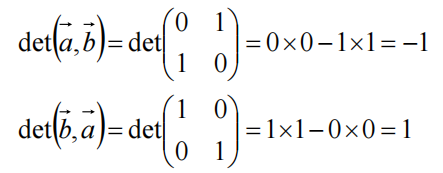
有向体积

（1）矩阵由三个向量构成，且如图10逆时针摆放，则行列式为正，是正体积，此时为右手坐标系 （2）矩阵由三个向量构成，且如图11顺时针摆放，则行列式为负，是负体积，此时为左手坐标系

证明行列式与有向体积相等

目标：对矩阵A，其列(行)向量张成的平行六面有向体积与A的行列式相等
证明思路————由“18-行列式性质与矩阵简化”中得到的结论：
对于矩阵A，定义一种运算F(A)，满足：
（1）任何一行数据，共同乘以c得到A`，则F(A`)=F(A)*c
（2）更换两行数据位置，得到A`，则F(A`)=-F(A)
（3）如果A是单位矩阵，则F(A)=1
（4）某一行数据乘以数字c，加到其他行上，得到A`，则F(A`)=F(A)
运算F(A)具有唯一性
如果能够证明体积的计算也满足上述性质，则可以确定体积的计算与行列式计算完全等同

证明性质(一)

任何一行数据，共同乘以k得到A`，则F(A`)=F(A)*k

1、把a与b向量张成的平面当作底面，c向其做高 2、当c向量乘以k得到kc向量 3、kc产生的高为k.h 4、所以得到的体积为原来的k倍 对于其他a和b向量，可以做同样的操作证明

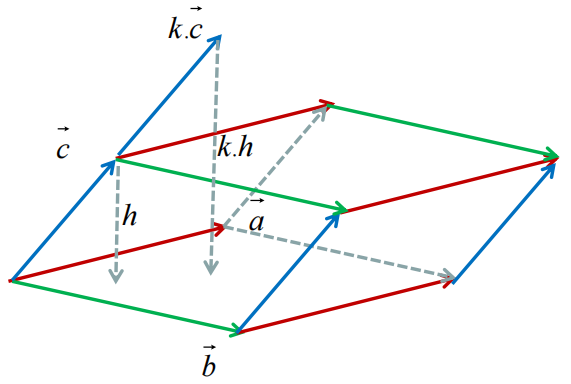
证明性质(二)

更换两行数据位置，得到A`，则F(A`)=-F(A)

1、假设当前矩阵中向量排列为顺序a-b-c 2、从图示角度看去，顺序为顺时针 3、当我们随意交换两个向量在矩阵中的排列位置 4、从图示角度看去，顺序为逆时针 所以改变矩阵中的向量排列，会改变有向体积符号

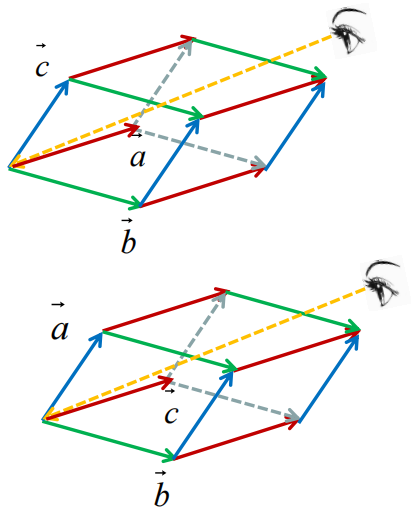
证明性质(三)

如果A是单位矩阵，则F(A)=1

1、当A为单位矩阵，abc按顺序排列为笛卡尔坐标系的xyz轴 2、abc长度为1，且两两垂直，其张成一个正方体，体积为1

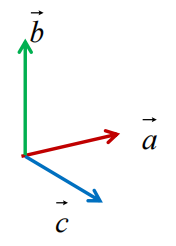
证明性质(四)

某一行数据乘以某一数字k，加到其他行上，得到A`，则F(A`)=F(A)

1、假设把a(或者b)乘以某一数字k，加到c上 2、向量c会产生如上图所示的变化 3、新构成的平行六面体底面积不变(ab构成) 4、由于c沿着ab构成的平面平行方向移动，所以到底面的高h不变 5、故本操作后，整体体积不变

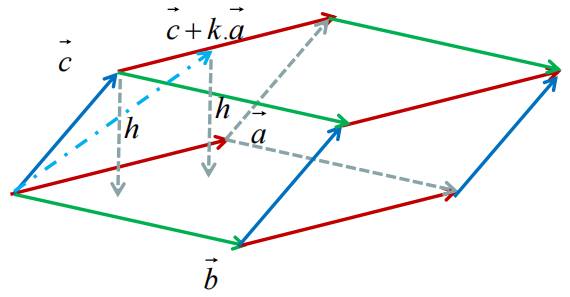
结论

以上过程，证明计算本平行六面体体积的函数F(A)满足初等变换性质，由F(A)的唯一性可知： 矩阵列(行)向量按序排列构成平行六面体的有向体积计算与其行列式计算等价