18-行列式性质与矩阵简化
回顾矩阵性质

可以观察到矩阵的上述性质与解N元一次方程的化简步骤类似:

对于方程组的系数矩阵,相当于应用了一系列初等变换,化简为一个单位阵:
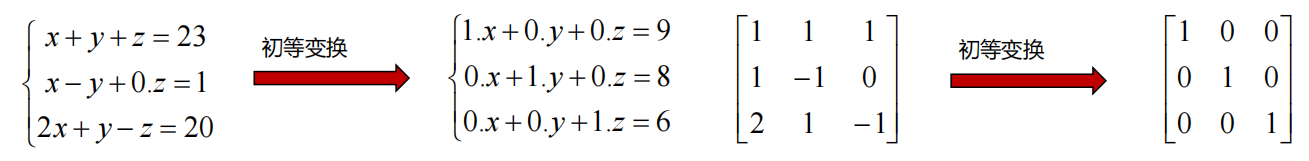
参考系数矩阵的行列式变化,根据矩阵行列式的性质,发现对行列式结果产生影响的操作如下:

应用行列式性质可知:
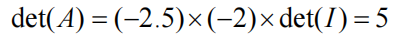
结论: 行列式不为0的矩阵,都可以通过初等变换,化简为单位矩阵
行列式计算唯一性
对于矩阵A,定义一种运算F(A),满足:

如果存在运算F,则运算得到的结果即为矩阵A的行列式;运算F对于矩阵A是否唯一?是否存在多个运算F满足上述性质?
简略证明行列式计算唯一性
假设对于方阵A,存在两种运算F0、F1,都可以满足行列式基本性质,求证:对于任意方阵A(行列式不为0),F0(A)=F1(A)
证明思路:
F0(A)与F1(A)都满足行列式基本性质
对A施加一系列初等变换,最终可以得到单位矩阵I
初等变换过程中,对F0(A)及F1(A)值的影响是相同的,假设最终影响因子是c
可知:
F0(A)=c*F0(I) F1(A)=c*F1(I)
由于二者都满足性质(单位矩阵的行列式为1)
则F0(A)=F1(A)=c
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
