如何绘制一个二维平面的三角形？

算法1：最小包围盒 + 向量积判断

得到最小包围这三个点的矩形，然后通过向量叉乘判断像素点是否在三角形内部，从而筛选出要绘制的像素点

void Application::rasterizeTriangle_vectorProduct( //包围盒向量积判断法
	std::vector<Point>& results,
	const Point& v0,
	const Point& v1,
	const Point& v2)
{
	//1.计算出最小包围盒
	int maxX = static_cast<int>(MAX(v0.x, MAX(v1.x, v2.x)));
	int maxY = static_cast<int>(MAX(v0.y, MAX(v1.y, v2.y)));

	int minX = static_cast<int>(MIN(v0.x, MIN(v1.x, v2.x)));
	int minY = static_cast<int>(MIN(v0.y, MIN(v1.y, v2.y)));

	//2.通过向量积作为三角形离散条件（判断像素点是否在三角形内部）
	math::vec2f pv0, pv1, pv2;
	Point result;
	for (int i = minX; i <= maxX; ++i) {
		for (int j = minY; j <= maxY; ++j) {
			pv0 = math::vec2f(v0.x - i, v0.y - j);
			pv1 = math::vec2f(v1.x - i, v1.y - j);
			pv2 = math::vec2f(v2.x - i, v2.y - j);

			auto cross1 = math::cross(pv0, pv1);
			auto cross2 = math::cross(pv1, pv2);
			auto cross3 = math::cross(pv2, pv0);

			bool negativeAll = cross1 < 0 && cross2 < 0 && cross3 < 0;
			bool positiveAll = cross1 > 0 && cross2 > 0 && cross3 > 0;

			if (negativeAll || positiveAll) {
				result.x = i;
				result.y = j;
				//interpolantTriangle(v0, v1, v2, result);
				results.push_back(result);
			}
		}
	}
}

算法2：最小包围盒 + 半平面方程增量符号判断

得到最小包围这三个点的矩形，然后通过半平面方程增量符号判断像素点是否在三角形内部，从而筛选出要绘制的像素点

void Application::rasterizeTriangle_halfSpaceEdge( //半平面增量式扫描线
	std::vector<Point>& results,
	const Point& v0,
	const Point& v1,
	const Point& v2)
{
	//1.计算出最小包围盒
	int maxX = static_cast<int>(MAX(v0.x, MAX(v1.x, v2.x)));
	int maxY = static_cast<int>(MAX(v0.y, MAX(v1.y, v2.y)));

	int minX = static_cast<int>(MIN(v0.x, MIN(v1.x, v2.x)));
	int minY = static_cast<int>(MIN(v0.y, MIN(v1.y, v2.y)));

	//2.三条边的半平面方程

	// 边 0: v0->v1, 内部用 v2 定符号
	// 边 1: v1->v2, 内部用 v0 定符号
	// 边 2: v2->v0, 内部用 v1 定符号
	struct Edge {
		int a, b, c;   // ax+by+c
	} edge[3];

	const Point* tri[3] = { &v0, &v1, &v2 };
	for (int i = 0; i < 3; ++i) {
		const Point& p0 = *tri[i];
		const Point& p1 = *tri[(i + 1) % 3];
		const Point& p2 = *tri[(i + 2) % 3];

		// 逆时针法向量 (a,b)
		edge[i].a = p0.y - p1.y;
		edge[i].b = p1.x - p0.x;
		edge[i].c = p0.x * p1.y - p1.x * p0.y;

		// 用第三个顶点确定“内侧”符号；若符号为负就整体反转
		int ref = edge[i].a * p2.x + edge[i].b * p2.y + edge[i].c;
		if (ref < 0) {
			edge[i].a = -edge[i].a;
			edge[i].b = -edge[i].b;
			edge[i].c = -edge[i].c;
		}
	}

	//3.计算包围盒左上角 (minX, minY) 的初始 F 
	int f0 = edge[0].a * minX + edge[0].b * minY + edge[0].c;
	int f1 = edge[1].a * minX + edge[1].b * minY + edge[1].c;
	int f2 = edge[2].a * minX + edge[2].b * minY + edge[2].c;

	//4. 扫描
	for (int y = minY; y <= maxY; ++y) {
		int rowF0 = f0;
		int rowF1 = f1;
		int rowF2 = f2;

		for (int x = minX; x <= maxX; ++x) {
			if (rowF0 >= 0 && rowF1 >= 0 && rowF2 >= 0) {
				results.push_back({ x, y });
			}

			// 行内 x 增量
			rowF0 += edge[0].a;
			rowF1 += edge[1].a;
			rowF2 += edge[2].a;
		}

		// 换行 y 增量
		f0 += edge[0].b;
		f1 += edge[1].b;
		f2 += edge[2].b;
	}
}

两种算法的用时对比

算法1，包围盒+向量积判断，用时:

图-1

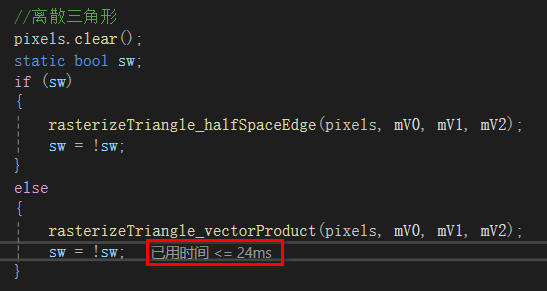
算法1，包围盒+半平面方程增量判断，用时:

图-2

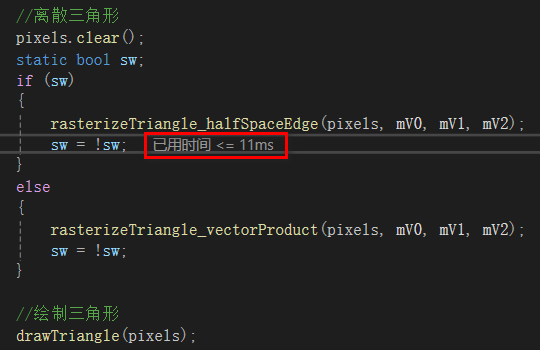
半平面方程算法梳理

1.通过三个顶点坐标得到最小包围盒，这是需要遍历筛选像素点的矩形区域

2.两个顶点坐标相减作为方向向量，根据p(x1-x0,y1-y0)，得到逆时针法向量n(y0-y1,x1-x0)

3.为什么要得到这个法向量呢？因为众所周知，半平面方程呢是 aX+bY+c=0、 aX+bY+c>0、 aX+bY+c<0这样式儿的，而其中的系数a和b就被规定为是aX+bY+c=0这条直线的法向量分量，也就是说，得到法向量n(y0-y1,x1-x0)就得到了这条两个顶点之间直线的a，b系数，既然得到了a=y0-y1，b=x1-x0，那代入直线上的(x0,y0)，就能求出c = -aX-bY = -(aX+bY) = -{(y0-y1)x0+(x1-x0)y0} = -{x0·y0 - x0·y1 + x1·y0 - x0·y0} = x0·y1 - x1·y0

4.求出了 a=y0-y1; b=x1-x0; c=x0·y1-x1·y0; 现在就可以把最小包围盒中的像素遍历依次代入到f=aX+bY+c中，就可以得到的f，f>0则表示这个点和直线法向量同向，f<0就是反向，f==0就是在直线上；但是在我们遍历之前需要再做一件必须要做的事，那就是需要把三角形的三条边表达式调整到法向量都指向三角形内部，这样后面通过他们的表达式才能判断出像素点是否在三角形内部

5.那aX+bY+c=0这条直线，怎么翻转它的法向量呢？那众所周知，只要把a、b、c三个系数取相反数就可以让这条直线的法向量指向相反方向。

6.现在已经把大部分要点说到了，还有最后一个要点：怎么遍历判断像素点的位置？真就每次都轮流代入三条边的直线方程然后判断结果值的正负吗？细心的朋友已经发现,在遍历时就是 f=a(X+1)+bY+c 实际就是 f=(aX+bY+c)+a，看到了吗？只需要加上一个法向量的分量a就相当于x+1位置的f，根据这个值来判断是否在三角形内部；y也是同理，当y+1换行时实际就是原来的f加上分量b；